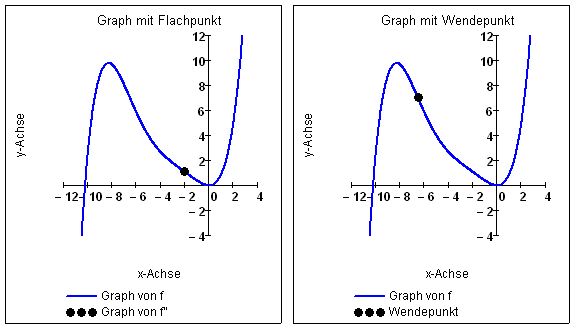
Im Rahmen der Kurvendiskussion gibt es Funktionen, deren zweite Ableitungsfunktion an der Stelle x0 eine einfache oder auch mehrfache Nullstelle hat. Man spricht dann von einer Flachstelle. In Abhängigkeit von der Vielfachhheit der Nullstelle kann diese Flachstelle auch eine Wendestelle sein. Die hinreichende Bedingung für die Art der Flachstelle ergibt sich aus der Vielfachheit der Nullstelle der zweiten Ableitung: Bei einer Nullstelle ohne Vorzeichenwechsel ändert sich das Krümmungsverhalten nicht, also Flachstelle, bei einer Nullstelle mit Vorzeichenwechsel ändert sich das Krümmungsverhalten, also Wendestelle.
Besitzt die Funktion an der Stelle x0 zusätzlich eine horizontale Tangente, so kann die Flachstelle eine Extremstelle sein (der Flachpunkt ist dann entweder ein Hochpunkt oder ein Tiefpunkt), oder aber eine Wendestelle mit horizontaler Tangente (der Wendepunkt ist dann ein Terrassenpunkt).
Flachpunkt und Wendepunkt