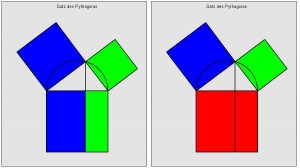
Der Satz des Pythagoras besagt: Die Summe der Flächeninhalte der Kathetenquadrate ist gleich dem Flächeninhalt des Hypotenusenquadrats.
Schon im alten Ägypten verwendeten die Seilspanner beim Bau der Pyramiden den Satz des Pythagoras. Mit Hilfe einer Zwölfknotenschnur erzielten sie einen genauen rechten Winkel: Ein langes Seil wird durch Knoten in 12 gleich lange Stücke geteilt und durch Pflöcke im Verhältnis
5:4:3 (Pythagoreisches Tripel) zu einem Dreieck aufgespannt. Dieses besitzt immer einen rechten Winkel (90°-Winkel).
Ein pythagoreisches Zahlentripel ist eine Menge von drei ganzen Zahlen, für die die Gleichung a2 + b2 = c2 gilt.
Dynamisch können diese Zahlentripel mit dem Computeralgebrasystem Mathcad generiert werden.
Darstellung pythagoreischer Zahlentripel mit Mathcad
Schulmathematische Anwendungen zum Satz des Pythagoras
pythagoras-1 pythagoras-2 pythagoras-mathcad


2 Kommentare
Pingback: Fermats letzter Satz | mathphys-online.de
Pingback: Pythagoras von Samos | mathphys-online.de